Na rysunku przedstawiono cząstkę (i stowarzyszoną z nią falę materii) padającą na skończoną barierę potencjału o szerokości L. Energia całkowita cząstki (E) jest mniejsza od wysokości bariery (V).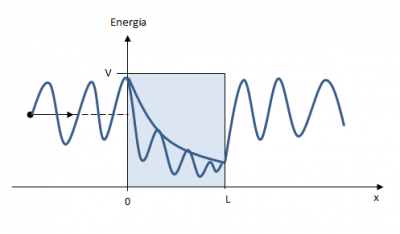
Amplituda fali materii wewnątrz bariery maleje w sposób wykładniczy. Jednak gdy cząstce uda się przejść przez barierę, to amplituda jej fali powraca do początkowej wartości, tak jak gdyby bariery w ogóle nie było.
Prawdopodobieństwo przejścia cząstki przez barierę scharakteryzowane jest przez tzw. współczynnik transmisji (T). Jeżeli np. jest on równy 0,2, to średnio 20% cząstek przeniknie przez barierę, a pozostałe 80% od niej się odbije.
Współczynnik transmisji opisuje w przybliżeniu funkcja wykładnicza w postaci:
\(T \approx e ^{-2kL} \)
gdzie:\(k= \sqrt{ \frac{2 \pi ^{2}m(V-E) }{h ^{2} } } \) , e – podstawa logarytmów naturalnych, m – masa cząstki, h – stała Plancka.
Z przedstawionych powyżej zależności wynika, że współczynnik transmisji bardzo silnie zależy od trzech zmiennych tj. masy cząstki, szerokości bariery oraz od różnicy energii bariery a energią cząstki.
Skończona bariera potencjału – przykład.
Wiązka elektronów o energii całkowitej 8•10-19J pada na barierę potencjału o szerokości 0,5nm i wysokości 11•10-19J. Ile wynosi przybliżone prawdopodobieństwo przejścia elektronu przez tą barierę?
Dane: Szukane:
E = 8•10-19J T = ?
L = 0,5nm = 0,5•10-9m
V = 11•10-19J
m = 9,1•10-31kg – masa elektronu
h = 6,63•10-34J•s – stała Plancka
Rozwiązanie:
Szukane prawdopodobieństwo jest współczynnikiem transmisji, który jest równy:
\(T \approx e ^{-2kL} \)
\(k= \sqrt{ \frac{2 \pi ^{2}m(V-E) }{h ^{2} } } \)
\(k= \sqrt{ \frac{2 \cdot 3,14 \cdot 9,1 \cdot 10 ^{-31}kg(11 \cdot 10 ^{-19}J-8 \cdot 10 ^{-19}J ) }{(6,63 \cdot 10 ^{-34} J \cdot s) ^{2} } } \)
\(k \approx 2 \cdot 10 ^{9} \frac{1}{m} \)
\(T \approx 2,7 ^{-2 \cdot 2 \cdot 10 ^{9} \frac{1}{m} \cdot 0,5 \cdot 10 ^{-9} m } =2,7 ^{-2} \approx 0,14\)
Otrzymany wynik oznacza, że na każde 100 elektronów przez barierę przejdzie około 14.