W odróżnieniu do fal biegnących amplituda fali stojącej jest zależna od położenia (x) danego elementu fali (w przypadku fal biegnących amplituda w każdym punkcie była identyczna) i wyraża się wzorem:
\(y=2Asin\left( \frac{2 \pi }{ \lambda } \cdot x\right)\)
gdzie: A – amplituda interferujących fal, λ – długość fali.
Jak wynika z równania amplituda fali stojącej osiąga wartość zero, tylko w przypadku, gdy funkcja sinus osiąga wartość zero. Jest to możliwe tylko wtedy, gdy argument funkcji sinus jest równy całkowitej wielokrotności π:
\( \frac{2 \pi }{ \lambda } \cdot x=n \pi \) gdzie: n = 0, 1, 2, …
Przekształcając ostatnie wyrażenie, otrzymamy wartości x, dla których amplituda fali jest równa zero, czyli miejsca gdzie znajdują się węzły fali stojącej.
\(x= \frac{n \lambda }{2} \)
Amplituda fali stojącej osiąga wartość maksymalną, równą 2A wówczas, gdy sinus osiąga swoją maksymalną wartość. Jest to spełnione dla argumentów spełniających warunek:
\( \frac{2 \pi }{ \lambda } \cdot x=(2n+1) \pi \) , gdzie n = 0, 1, 2, ….
Przekształcając równanie, otrzymamy położenia strzałek fali stojącej, czyli miejsc gdzie wychylenie fali osiąga wartość maksymalną, czyli 2A.
\(x= \frac{(2n+1)}{2} \cdot \lambda \)
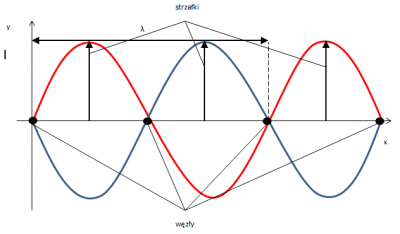
Na rysunku przedstawiono falę stojącą z zaznaczonymi węzłami i strzałkami.