Efekt Comptona polega na rozpraszaniu wysokoenergetycznych fotonów (promieniowania rentgenowskiego lub gamma), na swobodnych lub słabo związanych elektronach. W wyniku zderzenia fotonu z elektronem wzrasta długość fali fotonu, co można wytłumaczyć jedynie w oparciu o kwantową teorię promieniowania elektromagnetycznego. W zjawisku Comptona fotony przekazują elektronom zarówno swój pęd, jak i energię.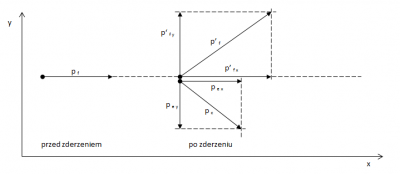
Na rysunku przedstawiono zderzenie fotonu ze swobodnym elektronem wraz z zaznaczonymi wartościami pędu obydwu cząstek przed i po zderzeniu.
W celu wyznaczenia wszystkich parametrów zjawiska Comptona należy skorzystać z zasad zachowania pędu i energii.
1. Zasada zachowania pędu w kierunku poziomym (wzdłuż osi x):
\(p _{f} =p' _{fx} +p _{ex} \)
Składowe pędu fotonu i elektronu wzdłuż osi x są odpowiednio równe:
\(p' _{fx} =p' _{f} \cdot cos \alpha \)
\(p _{ex} =p _{e} cos \beta \)
Wartości pędów obu cząstek po zderzeniu wynoszą:
\(p' _{f} = \frac{h}{ \lambda '} \)
\(p _{e} =mv\) , więc zasada zachowania pędu w kierunku poziomym ma postać:
\( \frac{h}{ \lambda } = \frac{h}{ \lambda '} \cdot cos \alpha +mvcos \beta \)
gdzie: h – stała Plancka, λ – długość fali fotonu przed zderzeniem, λ` - długość fali fotonu po zderzeniu, m – masa relatywistyczna elektronu, v – prędkość elektronu po zderzeniu.
2. Zasada zachowania pędu w kierunku pionowym (wzdłuż osi y):
\(0=p' _{fy} -p _{ey} \)
Składowe pędu fotonu i elektronu wzdłuż osi y są odpowiednio równe:
\(p' _{fy} =p' _{f} \cdot sin \alpha \)
\(p _{ey} =p _{e} \cdot sin \beta \) , stąd:
\(0=p' _{f} sin \alpha -p _{e} sin \beta \)
Zastępując pędy fotonu i elektronu odpowiednimi wyrażeniami otrzymamy:
\(0= \frac{h}{ \lambda '} \cdot sin \alpha -mvsin \beta \)
3. Zasada zachowania energii w postaci relatywistycznej:
\(E _{f}+E _{e} =E '_{f} +E' _{e} \)
\( \frac{hc}{ \lambda } +m _{0}c ^{2} = \frac{hc}{ \lambda '} +mc ^{2} \)
gdzie: m0 – masa spoczynkowa elektronu, c – prędkość światła w próżni.
Łącząc ze sobą trzy przedstawione powyżej równania i eliminując z nich wielkości, które dotyczą tylko elektronu, po dość skomplikowanych przekształceniach otrzymamy:
\( \lambda '= \lambda+ \lambda _{e} (1-cos \alpha )\)
gdzie: \( \lambda _{e} = \frac{h}{m _{0}e } =2,4263 \cdot 10 ^{-12}m \) - tzw. Comptonowska długość fali elektronu.
Z przedstawionej powyżej zależności wynika, że zmiana długości fali fotonu zależy jedynie od kąta pod jakim obserwuje się rozproszone promieniowanie elektromagnetyczne.