Włoskowatość jest zjawiskiem polegającym na podnoszeniu się lub obniżaniu poziomu menisku cieczy w cienkiej rurce (tzw. kapilarze), która jest zanurzona w cieczy, znajdującej się pod działaniem siły grawitacji.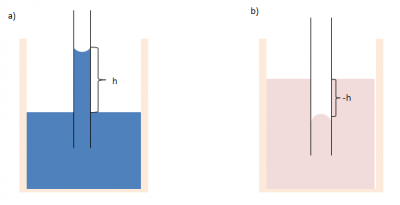 
Rys. 1. Włoskowatość cieczy w przypadku menisku a) wklęsłego, b) wypukłego.
W przypadku gdy, ciecz tworzy menisk wklęsły (tj. zwilża ścianki naczynia) poziom cieczy w kapilarze wzrasta. Gdy ciecz nie zwilża ścianek kapilary jej poziom ulega obniżeniu.
Zjawisko włoskowatości umożliwia wyznaczenie współczynnika napięcia powierzchniowego danej cieczy. W przypadku menisku wklęsłego ciężar cieczy (Q) o wysokości h w kapilarze jest równoważony przez siłę napięcia powierzchniowego (F). Odpowiednie siły są równe:
\(Q=mg= \pi r ^{2}h \rho g \)
\(F=2 \pi r \sigma \)
gdzie: m – masa słupa cieczy o wysokości h, g – przyspieszenie ziemskie, r – promień przekroju kapilary, ρ – gęstość cieczy, σ – współczynnik napięcie powierzchniowego.
Porównując ze sobą powyższe wyrażenia otrzymamy:
\(2 \pi r \sigma = \pi r ^{2} h \rho g\)
\( \sigma = \frac{rh \rho g}{r \rho g} \)
Jak wynika z ostatniego równania znajomość promienia kapilary, wysokości oraz gęstości cieczy umożliwia obliczenie współczynnika napięcia powierzchniowego cieczy. Przekształcając równanie względem h, otrzymamy:
\(h= \frac{2 \sigma }{r \rho g} \)
Zatem poziom cieczy jest tym większy, im mniejsza jest średnica kapilary.
Wyprowadzając powyższe wyrażenia przyjęto upraszczające założenie, że powierzchnie cieczy i rurki są do siebie styczne tzn. tworzą ze sobą kąt zero stopni. W rzeczywistości nie jest to prawdą, gdyż meniski tworzą ze ściankami naczynia pewien kąt α różny od 0, co powoduje, że równanie na σ należy dodatkowo podzielić przez cosinus tego kąta, tak więc w ogólnym przypadku:
\( \sigma = \frac{rh \rho g}{2cos \alpha } \) oraz \(h= \frac{2 \sigma cos \alpha }{r \rho g} \).
Zjawisko włoskowatości ma ogromne znaczenie dla przyrody, gdyż umożliwia przemieszczanie się ku górze płynów wewnątrz cienkich włókien roślin oraz wewnątrz szczelin w glebie. W oparciu o zjawisko włoskowatości działają knoty świec oraz tkaniny, których zadaniem jest jak najlepsze wchłanianie cieczy.