Na rysunku przedstawiono falę świetlną, która pada na przeszkodę w postaci dwóch bardzo wąskich szczelin, położonych w odległości d od siebie. Ugięte na każdej z szczelin fale interferują ze sobą kolejno konstruktywnie i destruktywnie, stąd na ekranie pojawia się obraz dyfrakcyjny, składający się z na przemian ułożonych jasnych i ciemnych prążków dyfrakcyjnych.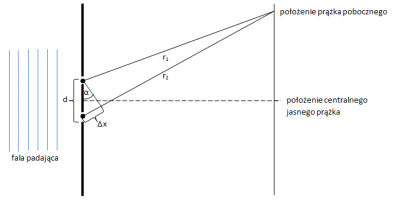
Powstawanie jasnych prążków dyfrakcyjnych jest rezultatem zjawiska interferencji konstruktywnej, które ma miejsce tylko wówczas gdy różnica dróg pomiędzy dwoma nakładającymi się na siebie falami (Δx) jest całkowitą wielokrotnością długości fali (λ), zatem:
\( \Delta x=n \lambda \)
gdzie: n = 1, 2, 3,… - numer rzędu widma.
Ponieważ \(sin \alpha = \frac{ \Delta x}{d} \) , to \( \Delta x=dsin \alpha \) . Położenie jasnego prążka dyfrakcyjnego rzędu n, musi więc być równe:
\(dsin \alpha =n \lambda \)
Pojawienie się ciemnych prążków dyfrakcyjnych jest konsekwencją interferencji destruktywnej, która ma miejsce tylko wówczas gdy różnica dróg pomiędzy dwoma nakładającymi się na siebie falami (Δx) jest całkowitą, nieparzystą wielokrotnością połowy długości fali (λ), zatem:
\( \Delta x=(2n+1) \frac{ \lambda }{2} \)
Ponieważ \( \Delta x=dsin \alpha \) , to położenie ciemnych prążków dane jest wzorem:
\(dsin \alpha =(2n+1) \frac{ \lambda }{2} \)
Dyfrakcja światła na dwóch szczelinach – przykład.
Znajdź długość fali, która pada na przeszkodę w postaci dwóch szczelin położonych w odległości 5μm wiedząc, że ciemny prążek drugiego rzędu obserwowany jest pod kątem 30°.
Dane: Szukane:
d = 5μm = 5•10-6m λ = ?
n = 2
α = 30°
Rozwiązanie:
\(dsin \alpha =(2n+1) \frac{ \lambda }{2} \)
\( \lambda = \frac{2dsin \alpha }{2n+1} = \frac{2 \cdot 5 \cdot 10 ^{-6}m \cdot sin30 ^{ \circ } }{2 \cdot 2+1} \)
\( \lambda =10 ^{-6} m\)