Strona główna

/

Zadania

/

Fizyka

/

Liceum

Współczynnik tarcia

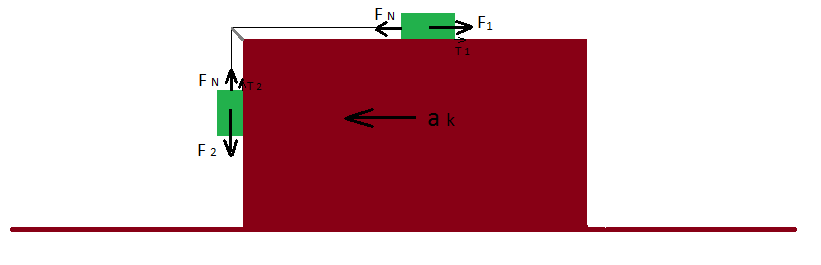
Na rysunku przedstawiono poruszający się drewniany klocek. Z jaką prędkością musiałby się poruszać, aby znajdujące się na nim masy m₁=5 kg i m₂=8 kgpozostały w spoczynku względem niego? Masa m₁ zaczepiona jest do nici, która poprzez obrotowy bloczek zaczepiona jest do masy m₂. Przyjmij, że współczynnik tarcia między drewnianym klockiem i masami wynosi f = 0,2. Można zaniedbać masę nici i obrotowego krążka oraz tarcie w samym krążku.

Liceum Fizyka

Odpowiedź eSzkola.pl

Justyna Ekspert eSzkola.pl

16.04.2020 10:29

Dane i szukane z zadania:

$m_1=5kg$

$m_2=8kg$

$g=10 \frac{m}{s^2}$

$a_k=?$

Jeżeli drewniany klocek będzie poruszał się w lewo, to na obie masy będą działały siły w prawo:

$F_1=m_1a_k$

oraz

$T_2=fN_2=f*m_2a_k$

na masę m₁ będzie działać dodatkowo siła tarcia, pochodząca od siły ciężkości:

$T_1=fN_1=f*m_1g$

Korzystając z drugiej zasady dynamiki Newtona, otrzymujemy równania ruchu:

$m_1a=F_N-T_1-F_1$

$m_2a=m_2g-fm_2a_k-F_N$

gdzie F_N to siła naciągu nici i jest zgodnie z II zadadą dynamiki takie same dla m₁ jak i m₂.

$0=F_N-T_1-F_1-m_1a$

$0=m_2g-fm_2a_k-F_N-m_2a$

Dodajemy otrzymane równania stronami:

$0=F_N-F_N+m_2g-m_1a_k-fm_1g-fm_2a_k$

$0=m_2g-m_1a_k-fm_1g-fm_2a_k$

$0=-a_k(m_1+fm_2)+g(m_2-fm_1)$

$a_k= \frac{g(m_2-fm_1)}{m_1+fm_2}$

$a_k= \frac{10 \frac{m}{s^2} (8kg-0,2*5kg)}{5kg+0,2*8kg} =2,57 \frac{m}{s^2}$

Odp. Minimalne przyspieszenie drewnianego klocka to 2,57 m/s².

Dzięki! 0

Znasz odpowiedź na to pytanie?

Wszystkie odpowiedzi (0)

Rozwiąż również: