Strona główna

/

Zadania

/

Matematyka

/

Liceum

Okrąg opisany na trapezie

Na trapezie $ABCD$ opisano okrąg o środku w punkcie $S$ i promieniu $r\ =\ 8\ \text{ cm}$ . Kąt między dłuższą podstawą $AB$ a promieniem okręgu poprowadzonym do punktu $A$ jest równy $30^{\circ}$ . Oblicz długości podstaw tego trapezu, jeśli jesgo wysokość jest równa $h\ =\ 10\ \text{ cm}$ .

Liceum Matematyka

Odpowiedź eSzkola.pl

Aleksandra Ekspert eSzkola.pl

17.07.2020 10:15

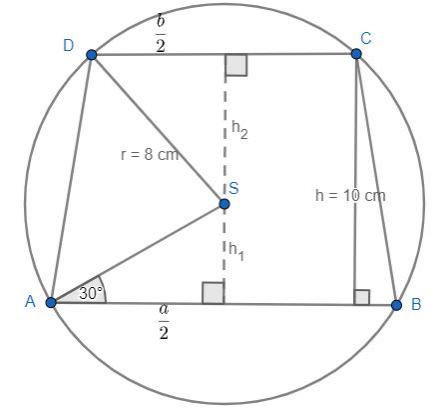
Poniższy rysunek jest ilustracją do zadania. Musimy wyznaczyć zaznaczone na nim długości $a\ \text{ i }\ b$ .

Na początku wyznaczymy długość podstawy $AB$ , korzytsając z wartości funkcji cosinus. Zaznaczamy odpowiedni trójkąt prostokątny i zapisujemy równanie.

$\cos 30^{\circ}\ =\ \frac{\frac{a}{2}}{8}$

$\frac{\sqrt[]{3}}{2}\ =\ \frac{a}{16}$

$a\ =\ 8\sqrt[]{3}\ \text{ cm}$

Teraz wyznaczamy wysokość $h_1$ , korzystając z tw. Pitagorasa.

$h_1^2\ +\ (\frac{a}{2})^2\ =\ r^2$

$h_1^2\ +\ (4\sqrt[]{3})^2\ =\ 8^2$

$h_1^2\ =\ 64\ -\ 48$

$h_1\ =\ 4\ \text{cm}$

Na kolejnym rysunku zaznaczono trójkąt prostokątny przy podstawie $CD$ . Korzystając z tw. Pitagorasa wyznaczymy długość $b$ .

Aby to zrobić, potrzebujemy długość wysokości $h_2$ .

$h\ =\ h_1\ +\ h_2$

$10\ \text{cm}\ =\ 4\ \text{ cm} +\ h_2$

$h_2\ =\ 6\ \text{ cm}$

Teraz zapisujemy tw. Pitagorasa

$h_2^2\ +\ (\frac{b}{2})^2\ =\ r^2$

$36\ +\ \frac{b^2}{4}\ =\ 64$

$b^2\ =\ 112$

$b\ =\ 4\sqrt[]{7}\ \text{ cm}$

Odp. Długości podstaw są równe $8\sqrt[]{3}\text{ cm}, \ 4\sqrt[]{7}\text{ cm}$ .

Dzięki! 0

Znasz odpowiedź na to pytanie?

Wszystkie odpowiedzi (0)

Rozwiąż również: