Rozwiązywanie nierówności wielomianowych

Rozwiąż nierówność

a) $3x^4+x^3+3x+1<0$ ,

b) $-x^3+2x^2-x>0$ .

Liceum Matematyka

Odpowiedź eSzkola.pl

Aleksandra Ekspert eSzkola.pl

24.03.2020 12:30

a) $3x^4+x^3+3x+1<0$

Szukamy pierwiastków wielomianu $3x^4+x^3+3x+1$ .

$w(x)=3x^4+x^3+3x+1=x^3(3x+1)+(3x+1)=(3x+1)(x^3+1)=3(x+\frac{1}{3})(x^3+1)$

Stosujemy wzór skróconego mnożenia na sumę sześcianów.

$w(x)=3(x+\frac{1}{3})(x+1)(x^2-x+1)$

Wyróżnik wielomianu $x^2-x+1$ jest ujemny, więc nie ma on pierwiastków rzeczywistych. Zatem, pierwiastkami wilomianu $w$ są $-\frac{1}{3}, \hspace{5pt} -1$ .

Szkicujemy wykres wielomianu. Zaznaczamy na osi pierwiastki wielomianu. Zaczynamy szkicowanie od prawej strony, jeśli przy najwyższej potędze jest współczynnik dodatni, to wykres rozpoczynamy po dodatniej stronie osi Y.

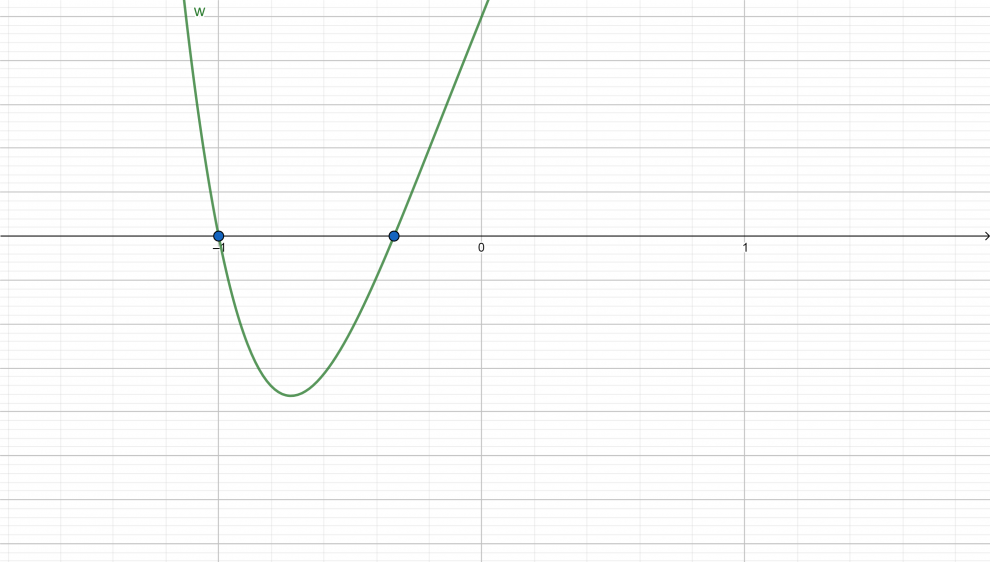
Z wykresu odczytujemy rozwiązanie nierówności $x\in(-1, -\frac{1}{3})$ .

b) $-x^3+2x^2-x>0$

Szukamy pierwiastków wielomianu $w(x)=-x^3+2x^2-x$ . Wyciągamy powtarzający się czynnik przed nawias, następnie zwijamy wyrażenie, stosując wzór na kwadrat sumy.

$w(x)=-x(x^2-2x+1)=-x(x-1)^2$

Zaznaczamy znalezione pierwiastki na osi ( $x_1=0, \hspace{5pt} x_2=1$ ). Szkicujemy wykres wielomianu zaczynając od lewej strony z ujemnej strony osi Y (poniważ współczynnik przy najwyższj potdze tego wielomianu jest ujemny). Przy pierwiastku podwójnym (tj. $x_2=1$ ) wykres odbija się od osi X (jest tak przy pierwiastkach krotności parzystej).

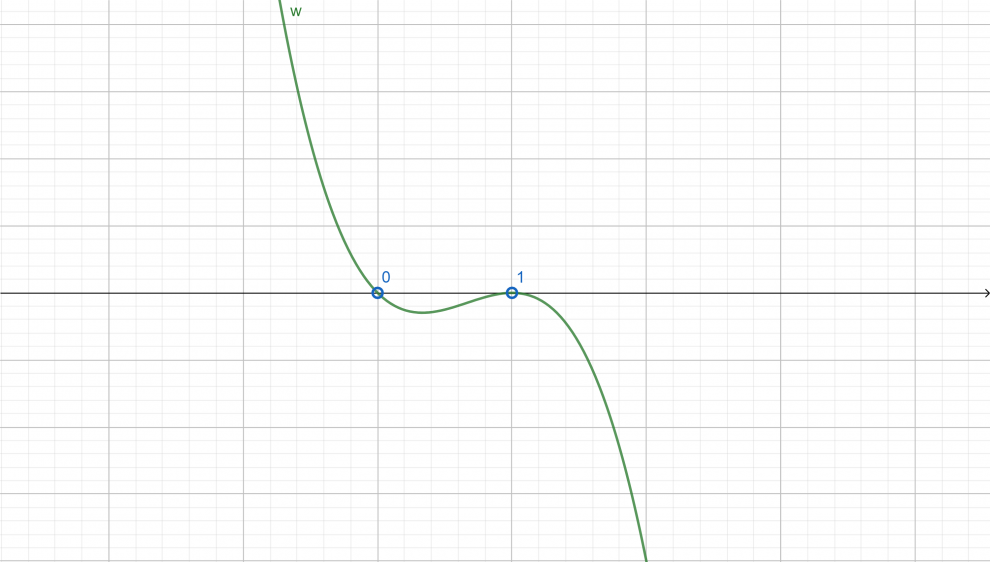
Z wykresu odczytujemy rozwiązanie $x\in(-\infty, \ 0)$ .

Dzięki! 0

Znasz odpowiedź na to pytanie?

Wszystkie odpowiedzi (0)

Rozwiązywanie nierówności wielomianowych

Odpowiedź eSzkola.pl

Rozwiąż również: