Przecięcie symetralnych boków trójkąta

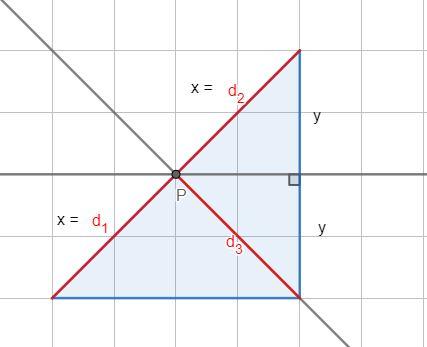
Rozpatrzymy na początku odległość punktu przecięcia symetralnych dwóch boków od wierzchołków trójkąta. Na poniższych rysunkach znajdują się przykłady dla trójkątów ostrokątnego, rozwartokątnego i prostokątnego. Punkt przecięcia symetralnych oznaczono literą , a rozważane odległości kolejno .

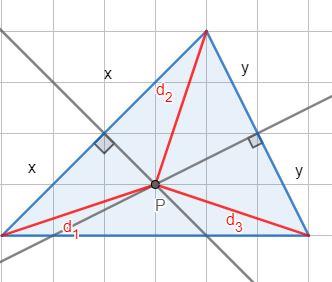
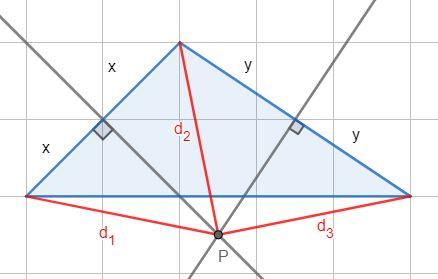
Zauważmy, że odległości  są równe, ponieważ są one przeciwprostokątnymi trójkątów prostokątnych o przyprostokątnych tych samych długości. Podobnie odległości  są takie same. Zatem

.

Przyjrzyjmy się teraz odległości punktu  od trzeciego boku trójkąta (którego symetralna nie została poprowadzona). W każdym z trzech przypadków odległość ta jest wysokością trójkąta równoramiennego o bokach długości . Ta wysokość oczywiście pada pod kątem prostym i przecina podstawę w połowie.

Zatem prosta przechodząca przez punkt  i spodek wysokości wspomnianego trójkąta równoramiennego jest symetralną trzeciego boku danego trójkąta.