gęstość cieczy

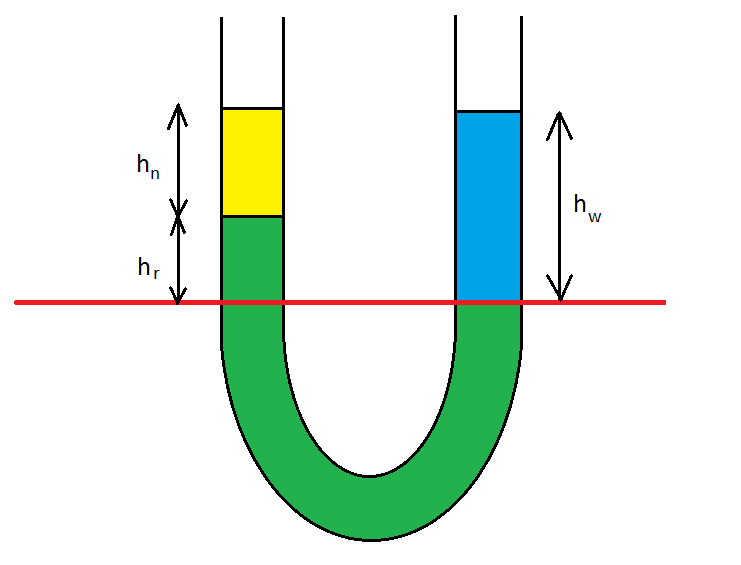
Jaś dostał od taty metrowy kawałek gumowej elastycznej i przezroczystej rurki. Wygiął ją w kształt litery U i do jednego z ramion tej rurki wlał rtęć (na rys kolor zielony), której gęstość wynosi 13600 kg/m³, a następnie wlał do tego samego ramiona nafty (na rysunku kolor żółty) o wysokości 10 cm, której gęstość wynosi 800 kg/m³. Ile powinien Jasio wlać (kolor niebieski) wody o gęstości 1000 kg/m³ do drugiego z ramion, aby górny poziom wody w jednym z ramion był równy górnemu poziomowi nafty w drugim ramieniu.

Liceum Fizyka

Odpowiedź eSzkola.pl

Justyna Ekspert eSzkola.pl

16.04.2020 05:19

Dane i szukane z zadania:

$h_n=10cm=0,1m$

$\rho _r=13600 \frac{kg}{m^3}$

$\rho _n=800 \frac{kg}{m^3}$

$\rho _w=1000 \frac{kg}{m^3}$

$h_w=?$

Ciśnienie na wysokości czerwonej lini na rysunku jest takie same ponieważ poniżej tego poziomu jest sama rtęć. W prawym ramieniu powyżej tej lini o wysokości h_w znajduję się tylko woda, na wysokości zaznaczonej lini woda ta wywiera takie same ciśnienie jak nafta o wysokości h_n i rtęć o wysokości h_r wiadomo, że:

$h_n+h_r=h_w$

Układ jest w równowadzę więc ciśnienie panujące w rurce na wysokości czerwonej linii w obu ramionach jest takie samo

$p _r+ p_n= p _w$

Korzystając z wzoru na ciśnienie hydrostatyczne powyższe równanie zapisujemy w postaci równania:

$\rho _rh_rg+ \rho _nh_ng= \rho _wh_wg$

$\rho _rh_r+ \rho _nh_n= \rho _wh_w$

$h_r=h_w-h_n$

$\rho _r(h_w-h_n)+ \rho _nh_n= \rho _wh_w$

$\rho _rh_w- \rho _rh_n+ \rho _nh_n= \rho _wh_w$

$- \rho _rh_n+ \rho _nh_n= \rho _wh_w- \rho _rh_w$

$- \rho _rh_n+ \rho _nh_n= h_w(\rho _w- \rho _r)$

$\frac{- \rho _rh_n+ \rho _nh_n}{\rho _w- \rho _r} = h_w$

$h_n(\frac{- \rho _r+ \rho _n}{\rho _w- \rho _r}) = h_w$

Podstawiamy dane z zadania

$h_w=0,1m* \frac{-13600 \frac{kg}{m^3}+ 800 \frac{kg}{m^3} }{1000 \frac{kg}{m^3}-13600 \frac{kg}{m^3}} =0,1m* \frac{-12800 \frac{kg}{m^3} }{-12600 \frac{kg}{m^3}}=0,1m* \frac{128}{126} =0,102m$

Odp. Wysokość słupa wody wynosi 0,102m

Dzięki! 1

Znasz odpowiedź na to pytanie?

Wszystkie odpowiedzi (0)

gęstość cieczy

Odpowiedź eSzkola.pl

Rozwiąż również: